参考

参考自https://www.cnblogs.com/wl-blog/p/14913905.html，这篇讲的很清楚。

先上代码：

1
2
3
4
5
6
7
8
9
10
11
# N = 4
# V = 5
# obj = [[1, 2], [2, 4], [3, 4], [4, 5]]

value = [[0 for j in range(V + 1)] for i in range(N + 1)]

for item in range(1, N + 1):
    for volume in range(1, V + 1):
        value[item][volume] = value[item - 1][volume]
        if volume >= obj[item - 1][0] and value[item][volume]< value[item - 1][volume - obj[item - 1][0]] + obj[item - 1][1]:
            value[item][volume] = value[item - 1][volume -obj[item - 1][0]] + obj[item - 1][1]

大致思路：

一个背包在只能选择n-1个物品时达到了最优解，如果此时可以选择第n个物品了(假设剩余容积可以放下该物品)，那么最优解就可以分成两个可能：选择第i个物品和不选择第i个物品

于是就可以通过定下初始条件进行递推

1
2
# 状态转移方程
f[i][v]=max{ f[i-1][v], f[i-1][v-w[i]]+v[i] }

如果不选择第i个物品，那么最大价值和f[i-1][v]相同

如果选择第i个物品，最大价值=容量为v-w[i]时的最大价值（最优解）+i物品的价值

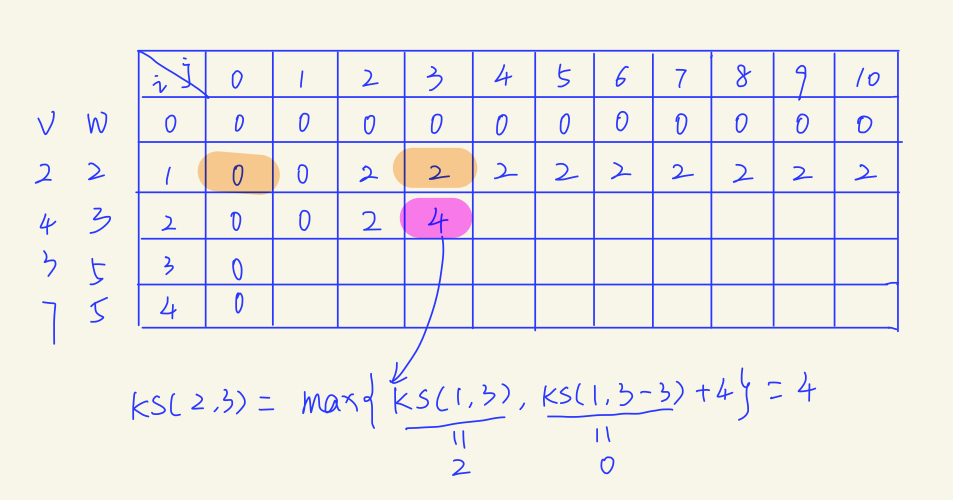
好图，偷了