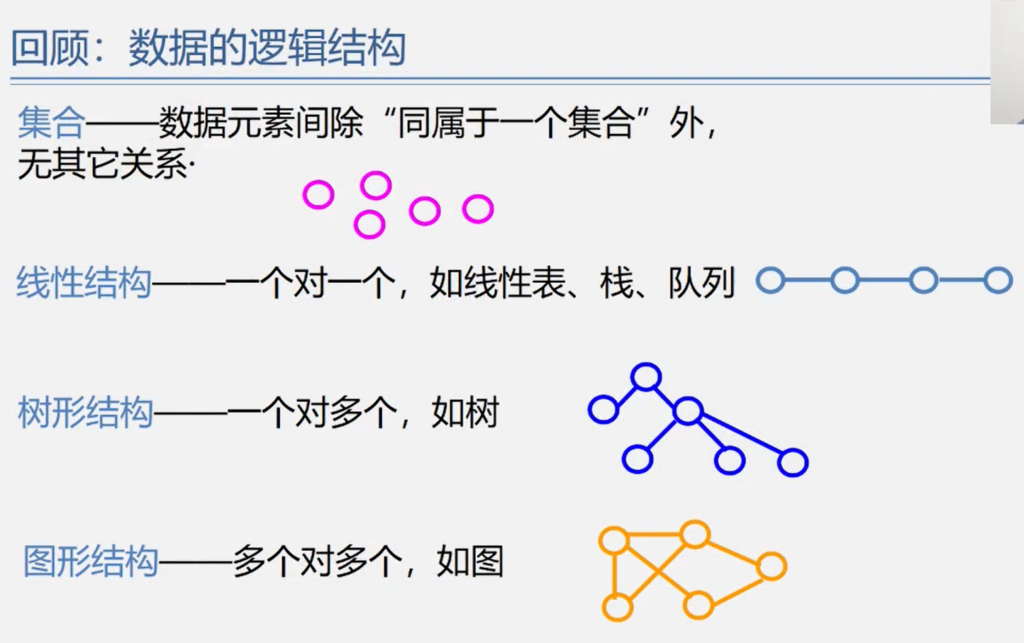
四种逻辑结构

图的定义

G=(V,E)

Graph=(Vertex,Edge)

图=顶点的有穷集合+边的有穷集合

图的种类

无向图/有向图

完全图/稠密图/稀疏图

网：边/弧带权的图

图的术语

顶点的度：与该顶点关联的边的数目，在有向图中则细分为入度和出度

路径：持续的边构成的顶点序列

连通图：任何两顶点均存在路径

子图：顶点集合或者边为父图的子集合的图

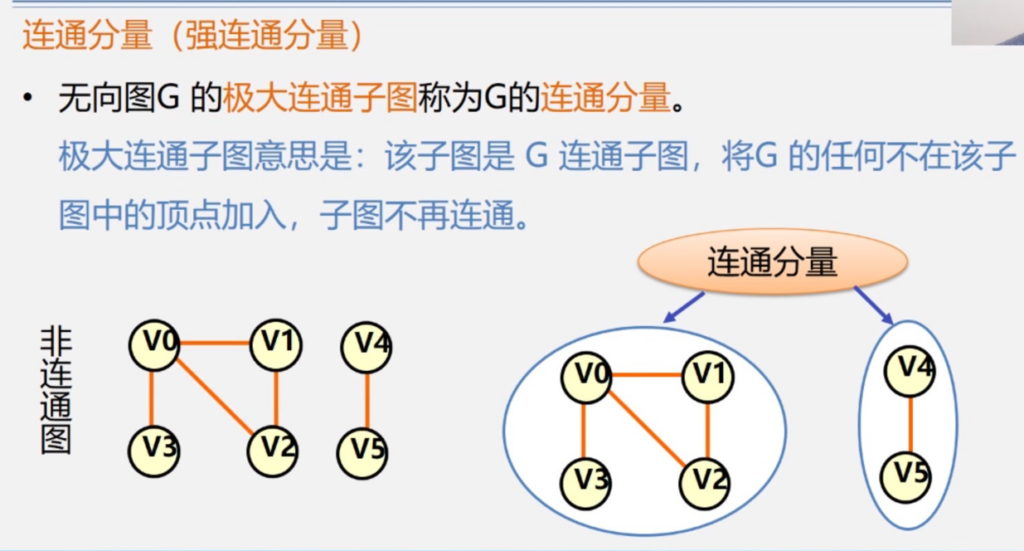
可以说是很不说人话了

人话就是，彼此不相连的，不可分割的个体。

图的遍历

分为深度优先遍历和广度优先遍历，后面展开讲

图的存储结构

邻接矩阵

建立一个顶点表存储顶点信息，再建立一个邻接矩阵记录个顶点的关系（也就是边或者弧）

  • 无向图的邻接矩阵是对称的——甲能到达乙，乙自然可以到达甲（可以压缩存储空间）
  • 顶点的度就是该行的“1”的数目
  • 对于有向图，入度是该行“1”的数目，出度是该列的“1”的数目
  • 对于有权图，不相邻的两顶点，矩阵对应值为“∞”

邻接矩阵的缺点

  • 不便于增加删除
  • 浪费空间（稀疏）
  • 浪费时间——统计有多少边时